 |
 |
|
|
|
|
|
|
|
|
<< Preceding Page |
|
|
|
|
 |
IV. Fractal-Kinetic Theory
(1/3 Pages) |
|
|
|
|
|
|
1. Dynamic Fractal Theory
Because existing fractal theory cannot explain dynamic fractal movement, we need new fractal theory that can explain it. A human body works as a dynamic fractal system, and causes disease by using the dynamic fractal mechanisms. Thus, it is necessary that we make dynamic fractal theory which can explain how a human body and the tissue controls the internal conditions. This is the purpose of "Fractal-Kinetic Theory."
(a) Definition of Internal Cellular Movement
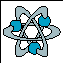
First of all, make the dynamic model of a gauge. A cell, in the section of "Gauge and Field," has already been defined as a gauge; however, it does not contain its own movement. Thus, let us decide internal cellular movement, and add it to a gauge. A cell has stable metabolic movement, so that it can be regarded as a stable physical movement. In addition, a circular motion is one of the representative stable movements in nature. Thus, let us add a circular motion to a gauge, and define a cell as a gauge having a circular motion. I call this gauge "Dynamic Gauge." This is the first step for us to form "Fractal Kinetic Theory." |
|
|
|
|
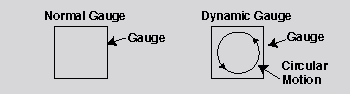 |
|
(A cell can be regarded as an independent system, so that it can be defined as a gauge. In addition, a cell contains stable metabolic movement, so that it can be defined as a gauge having a circular motion. ) |
|
|
|
|
(b) Definition of Internal Fractal Movement
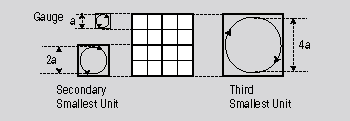
Next, decide the sizes of fractal movements in fractal units. A fractal unit changes the size according its belonging level. In addition, a fractal unit can be considered to contain its own internal movement according the size of the fractal unit. These two indications allow us to determine the internal movement of a fractal unit as follows. The secondary-smallest fractal unit contains a circular motion whose diameter is twice as large as that of a circular motion in a dynamic gauge. The third-smallest fractal unit contains a circular motion whose diameter is four times as large as that of a circular motion in a dynamic gauge. Using these different-sized circular motions enables us to express how a tissue changes its metabolic turnover rate. The figure below shows how a fractal unit contains its own movement according its level.
|
| (A fractal structure consists of different-sized units, each of which contains the internal movement that is directly proportional to the size of the fractal unit. Thus, in the fractal structure illustrated in the figure above, the secondary-smallest unit contains movement of which size is twice as large as that of the smallest unit. The third-smallest unit contains movement of which size is twice as large as that of the secondary-smallest unit. This model, of course, indicates the basic model of a fractal structure. ) |
|
|
|
|
|
MyBook

PDF File Download

(Donation Ware)
SugiInternalMedicineClinic
MIKIOSUGI: 杉幹雄
Present Japan Time:
2026/01/13 (Tue) 02:29:53 |
|