 |
 |
|
|
|
|
|
|
|
|
<< Previous Page |
|
|
|
|
 |
VI. Dimensional-Gauge Theory
(1/3 Pages) |
|
|
|
|
|
|
|
Dimensional-Gauge Theory explains that "A normal cell and a cancer cell belongs to different levels." This indication can be lead through three steps. First of all, let us check what stability a normal and a cancer cell have. Next, compare the momentum contained in a cancer cell with that contained in a normal cell. Lastly, by using theoretical models, try to express theoretically both a normal and a cancer cell.
1. Three-Dimensional Stability
"Whereas a normal cell does not have three-dimensional stability, a cancer cell has it." This indication can be deduced from a phenomenon: whereas a normal cell has anchorage dependence, a cancer cell does not have it.
(a) A normal cell and the internal movement
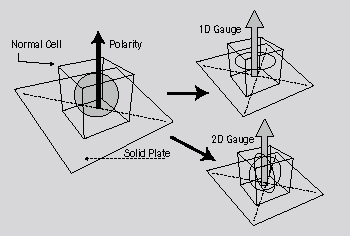
A normal cell can be considered to need anchorage dependence in order to obtain three-dimensional stability. When a cell is on a solid plate, it can obtain a polarity that is perpendicular to the solid plate. By using the polarity, the normal cell can fix the internal movement, and can start its cell division. This suggests that a normal cell contains movement that is not adaptable for three-dimensional space. All in all, it is indicated that a normal cell does not have three-dimensional stability, and contains one or two-dimensional movement.
The figures below illustrate that two kinds of normal cells. One is a normal cell containing movement controlled by one-dimensional movement; the other is that containing movement controlled by two-dimensional movement. These two cells, as shown in the figures below, can obtain three-dimensional stability by attaching to a solid plate. |
|
|
|
|
 |
|
(A normal cell, by using anchorage dependence, gets a polarity, which allows internal movement in the cell to fix to the three-dimensional movement in the space.) |
|
|
|
|
(b) A cancer cell and the internal movement
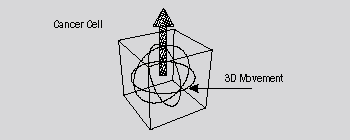
A cancer cell, different from a normal cell, does not need anchorage dependence, because it has three-dimensional stability from the birth. A cancer cell has the internal movement having three-dimensional stability. Thus, without using attaching to a solid plate, a cancer cell can divide itself. Additionally, movement that is stable in the three-dimensional space is three-dimensional movement. Thus, it is concluded that a cancer cell contains movement controlled by three-dimensional movement. The figure below illustrates this mechanism. |
|
|
|
|
|
|
(A cancer cell contains three-dimensional movement, so that it can be considered to have three-dimensional stability without attaching to a solid plate.) |
|
|
|
|
(c) Three-dimensional stability and Cell division
A cell needs three-dimensional stability to divide itself. A cell lives in time and space, and it needs to enlarge its volume by adapting to the space movement which indicates three-dimensional movement. In addition, a movement having three-dimensional stability is only three-dimensional movement. Thus, a cell needs three-dimensional stability when it divides itself. That is, because a normal cell does not have three-dimensional stability, it needs anchorage dependence to obtain the stability. |
|
|
|
|